Sequência de Fibonacci

Para os que gostam de Matemática, é uma boa curiosidade.

A sucessão de Fibonacci ou sequência de Fibonacci é uma sequência de números naturais, na qual os primeiros dois termos são 0 e 1, e cada termo subsequente corresponde à soma dos dois precedentes. Fibonacci considerou o crescimento de uma população idealizada (não realista biologicamente) de coelhos. Os números descrevem o número de casais na população de coelhos depois de n meses se for suposto que:

• no primeiro mês nasce apenas um casal,
• casais amadurecem sexualmente (e reproduzem-se) apenas após o segundo mês de vida,
• não há problemas genéticos no cruzamento consanguíneo,
• todos os meses, cada casal fértil dá a luz a um novo casal, e
• os coelhos nunca morrem.

Em termos matemáticos, a sequência é definida recursivamente pela fórmula abaixo, sendo os dois primeiros termos F₀= 0 e F₁= 1.

Com esta fórmula podemos montar a sequência de Fibonacci e descobrir, por exemplo, quantos coelhos foram gerados no sexto mês, basta aplicar a fórmula descrita acima até chegar ao ponto inicial de 1 e 1, como mostra a figura abaixo:

 F(6) = F(6 - 1) + F(6 - 2)  >>>
 F(6) = F(5) + F(4) >>>  'Agora, faz as mesmas operações com F(5) e F(4)'
 F(6) = F(5 - 1) + F(5 - 2) + F(4 - 1) + F(4 - 2) >>>
 F(6) = F(4) + F(3) + F(3) + F(2) >>> 'Continua, agora com as funções F(2) a F(4)'
 F(6) = F(3) + F(2) + F(3 - 1) + F(3 - 2) + F(3 - 1) + F(3 - 2) + F(2 - 1) + F(2 - 2) >>>
 F(6) = F(3) + F(2) + F(2) + F(1) + F(2) + F(1) + F(1) + 0 >>>>
 F(6) = F(2) + F(1) + F(1) + F(1) + 1 + F(1) + 1 + 1 + 0 >>>
 F(6) = F(1) + 1 + 1 + 1 + 1 + 1 + 1 + 1 >>>> 'Substitui nossa premissa, e...'
 F(6) = 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 = 8

Ou seja, no sexto mês foram gerados 8 coelhos.

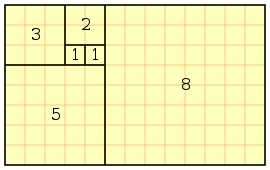
Note que a sequência de Fibonacci está no resultado de cada posição da figura: 1, 1, 2, 3, 5, 8, ...

A sequência de Fibonacci tem aplicações na análise de mercados financeiros, na ciência da computação e na teoria dos jogos. Também aparece em configurações biológicas, como, por exemplo, na disposição dos galhos das árvores ou das folhas em uma haste, no arranjo do cone da alcachofra, do abacaxi,ou no desenrolar da samambaia.

Ah! A sequência de Fibonacci pode ser encontrada também  no Triângulo de Pascal.